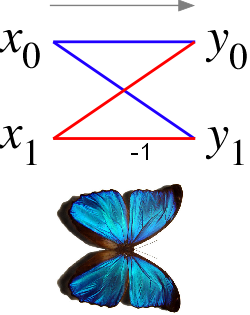Accelerate clusters with flattened butterflies

On 11 Feb, 2015 By michaelmalak 0 Comments
michaelmalak's picture

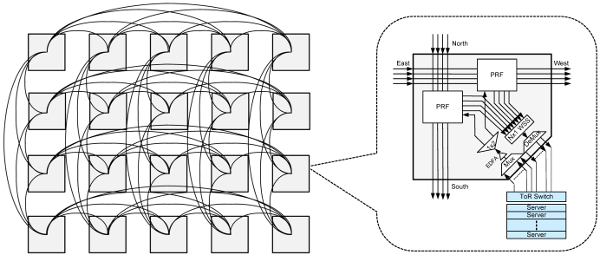
A new Hadoop/Spark network topology published last week, Fully programmable and scalable optical switching fabric for petabyte data center, demonstrated a 10% speedup. Instead of the typical "fat tree" network topology, this technique uses a "compressed butterfly". Because that increases the radix (fan-out), they also switched to optical networking to accommodate it. But it's interesting because they were able to achieve this speedup without any changes to the software, such as regarding data locality.

The topology that is being changed here is rack-to-rack. Within a single rack, there's still just a top-of-rack switch that connects all the nodes (computers) in it.

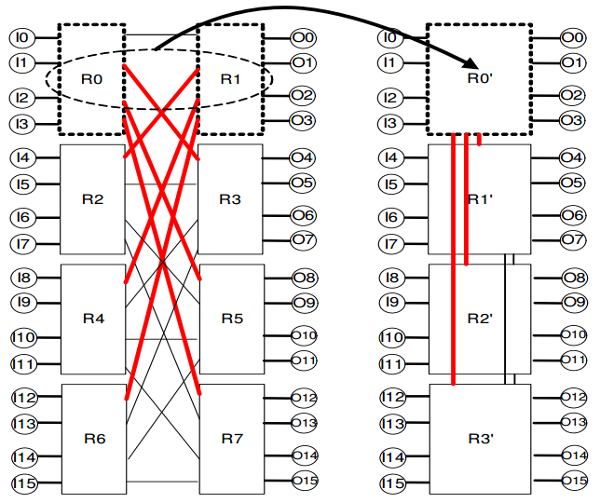
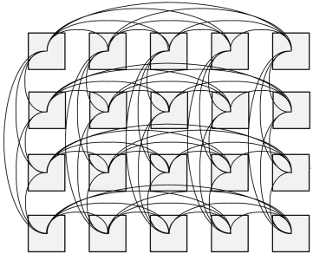
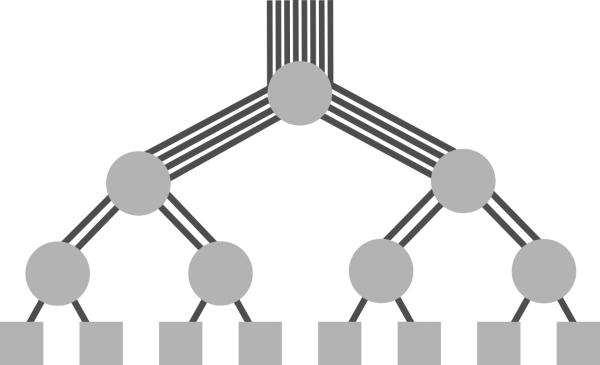
The typical "fat tree" topology in a Hadoop/Spark cluster is strictly hierarchical. The switches higher in the tree receive greater network traffic and pressure, and thus have to be beefier and more expensive. The flattened butterfly, in contrast is more peer-to-peer and avoids the "core" switch(es) at the top/upper layers of the fat tree.

Fat tree diagram from clusterdesign.org

The flattened butterfly has an interesting history that traces back over 200 years to Carl Friedrich Gauss. Although the term "butterfly" wasn't coined until 1969, Gauss discovered the formulas that would eventually be represented as a butterfly diagram. Then in the 1980's,

  • 1805 Carl Friedrich Gauss develops what would later be known as Fourier analysis, as well as computational formulas similar to what Cooley and Tukey would rediscover in 1965.
  • 1807 Joseph Fourier independently discovers what would later be known as Fourier analysis.
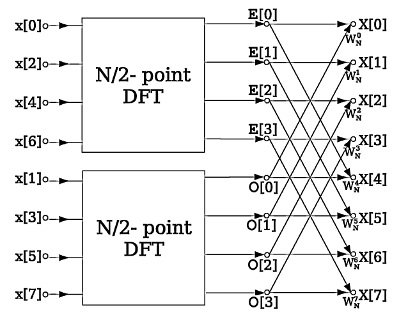
  • 1965 Cooley and Tukey develop the FFT algorithm.
  • 1969 MIT Lincoln Labs coins the Cooley-Tukey diagram as being a "butterfly diagram".
  • 1986 NASA Ames is inspired by the FFT butterfly to connect the nodes in a parallel computer in a similar fashion for general purpose computing (although many others for several years previously connected processors or computers in a butterfly data flow arrangement simply to compute the FFT).
  • 2007 Stanford and Cray develop the flattened butterfly for the network of a cluster of computers.
  • 2010 Google paper shows the energy efficiency of the flattened butterfly.
  • 2015 Zhu et al measure the performance of the flattened butterfly on an Apache Spark cluster.

Or, more diagrammatically:

1. Original 2-point FFT butterfly, a representation of Gauss's original 1805 formulas. From wikimedia

 

2. An 8-point version of the above. From wikimedia

 

3. Butterfly adapted to inter-processor communication. 4. Flattened butterfly (each row has its columns merged). From Kim et al 2007

 

5. Flattened butterfly applied to a mesh of racks. From Zhu et al 2015